

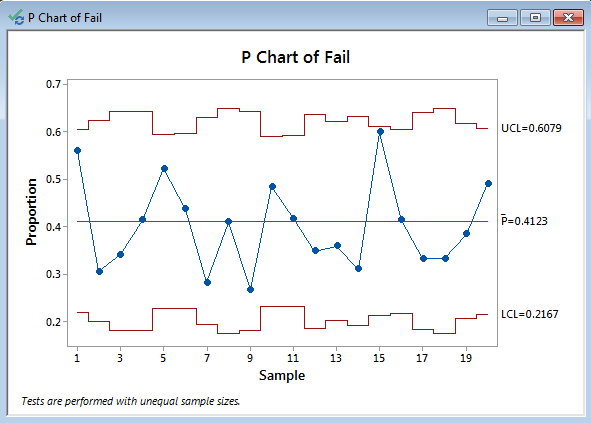
It is never appropriate to conclude that changes in one variable cause changes in another based on correlation alone.
The relationship is negative because as one variable increases, the other variable decreases. The points fall close to the line, which indicates that there is a strong relationship between the variables. Strong negative relationship: Spearman rho = 1.0 The relationship is positive because the variables increase concurrently. Strong positive relationship: Spearman rho = 0.948 The points fall randomly on the plot, which indicates that there is no relationship between the variables. The following plots show data with specific Spearman correlation coefficient values to illustrate different patterns in the strength and direction of the relationships between variables. For example, a Spearman correlation of −1 means that the highest value for Variable A is associated with the lowest value for Variable B, the second highest value for Variable A is associated with the second lowest value for Variable B, and so on.
The larger the absolute value of the coefficient, the stronger the relationship between the variables.įor the Spearman correlation, an absolute value of 1 indicates that the rank-ordered data are perfectly linear. The correlation coefficient can range in value from −1 to +1. Then, Minitab calculates the correlation coefficient on the ranked data. To calculate the Spearman correlation, Minitab ranks the raw data. In a monotonic relationship, the variables tend to move in the same relative direction, but not necessarily at a constant rate. Use the Spearman correlation coefficient to examine the strength and direction of the monotonic relationship between two continuous or ordinal variables. The relationship is negative because, as one variable increases, the other variable decreases. The points fall close to the line, which indicates that there is a strong negative relationship between the variables. Large negative relationship: Pearson r = −0.968 The relationship is positive because as one variable increases, the other variable also increases. The points fall close to the line, which indicates that there is a strong linear relationship between the variables. Large positive relationship: Pearson r = 0.93 Some points are close to the line but other points are far from it, which indicates only a moderate linear relationship between the variables. Moderate positive relationship: Pearson r = 0.476 The points fall randomly on the plot, which indicates that there is no linear relationship between the variables. The following plots show data with specific correlation values to illustrate different patterns in the strength and direction of the relationships between variables.

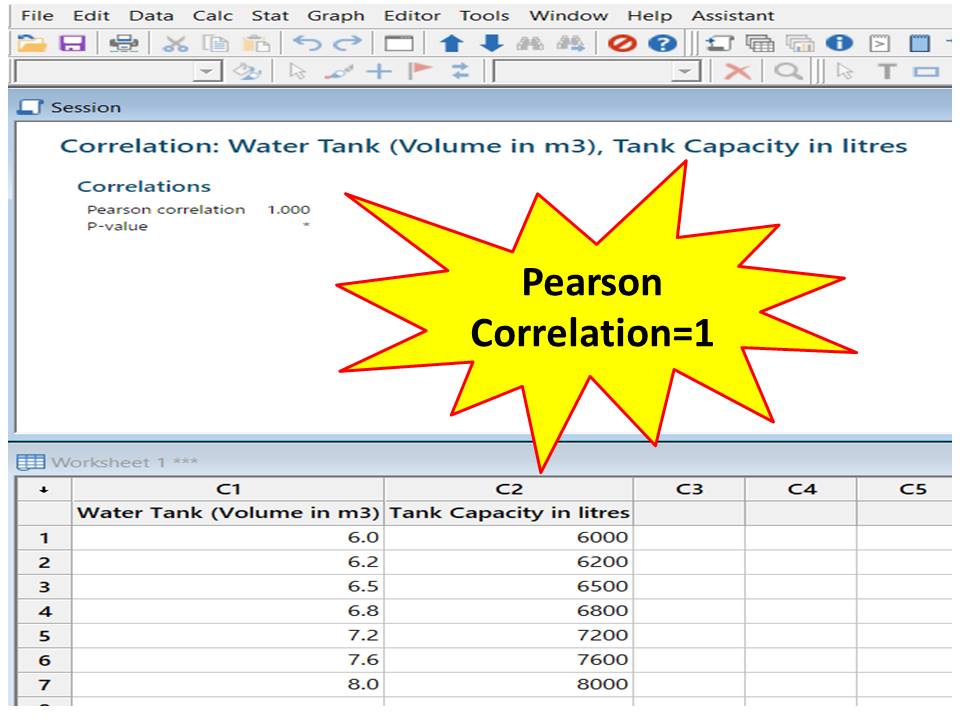
If one variable tends to increase as the other decreases, the coefficient is negative, and the line that represents the correlation slopes downward. If both variables tend to increase or decrease together, the coefficient is positive, and the line that represents the correlation slopes upward. The sign of the coefficient indicates the direction of the relationship. A correlation close to 0 indicates no linear relationship between the variables. For the Pearson correlation, an absolute value of 1 indicates a perfect linear relationship. The larger the absolute value of the coefficient, the stronger the relationship between the variables. Use the Pearson correlation coefficient to examine the strength and direction of the linear relationship between two continuous variables.


 0 kommentar(er)
0 kommentar(er)
